Sistemas Lineares Brasil Escola – Desvendando a Álgebra

Sistemas Lineares: O Que São, Como Resolver, Tipos – Brasil Escola. Embarque conosco numa jornada fascinante pelo mundo dos sistemas lineares! Descubra como essas estruturas matemáticas, aparentemente complexas, são a chave para solucionar problemas em diversas áreas, desde a engenharia e a economia até o planejamento urbano e a ciência da computação. Prepare-se para desvendar os métodos de resolução, compreender os diferentes tipos de sistemas e suas implicações geométricas, e aplicar esse conhecimento em situações práticas do dia a dia.

A elegância e a potência dos sistemas lineares estão prestes a serem reveladas.

Neste texto, exploraremos o conceito de sistemas lineares de forma clara e acessível, desvendando a sua aplicação em diferentes contextos. Aprenderemos a resolver sistemas lineares utilizando métodos como substituição, adição, regra de Cramer e o método de Gauss-Jordan. Vamos diferenciar os tipos de sistemas lineares – possível, impossível e indeterminado – analisando suas características e representações geométricas. Ao final desta jornada, você terá uma compreensão sólida e abrangente desse tema fundamental da matemática.

Métodos de Resolução de Sistemas Lineares

A jornada pela resolução de sistemas lineares se abre diante de nós, revelando um universo de métodos elegantes e poderosos. Cada técnica, uma ferramenta precisa para desvendar o enigma das incógnitas interligadas. A escolha do método ideal dependerá da complexidade do sistema e da preferência do solucionador, mas todos convergem para o mesmo objetivo: encontrar a solução que harmoniza todas as equações.

Método de Resolução por Substituição, Sistemas Lineares: O Que São, Como Resolver, Tipos – Brasil Escola

Este método, de simplicidade quase poética, consiste em isolar uma variável em uma das equações e substituí-la nas demais, reduzindo gradualmente o número de incógnitas até encontrar a solução. Vejamos sua aplicação em sistemas 2×2 e 3×3.

Sistema 2×2

Considere o sistema:

x + y = 5
x – y = 1

Isolando x na segunda equação, temos x = y +

1. Substituindo na primeira equação

(y + 1) + y = 5. Resolvendo para y, obtemos y = 2. Substituindo y = 2 na equação x = y + 1, encontramos x = 3. Portanto, a solução é x = 3 e y = 2.

Sistema 3×3

Para um sistema 3×3, o processo se repete, porém com mais etapas. Considere o sistema:

x + y + z = 6
x – y + z = 2
x + y – z = 0

Isolando x na terceira equação, temos x = z – y. Substituindo em ambas as outras equações, eliminamos x e obtemos um sistema 2×2 em y e z. Resolvendo este sistema, encontramos os valores de y e z, e posteriormente, substituindo em x = z – y, encontramos o valor de x. O raciocínio é análogo ao do sistema 2×2, mas com mais iterações.

Método de Resolução por Adição

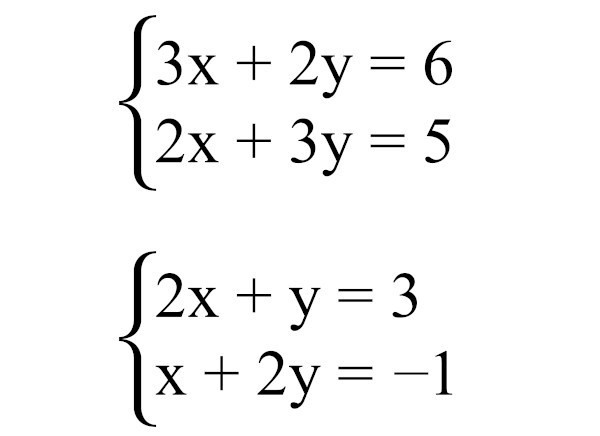
O método da adição, também conhecido como método da eliminação, se baseia na manipulação algébrica das equações para eliminar variáveis. Somamos ou subtraímos as equações, multiplicando-as previamente por constantes se necessário, visando simplificar o sistema.

Sistema 2×2

Considere o sistema:

2x + y = 7
x – y = 2

Somando as duas equações, eliminamos y: 3x = 9, logo x = 3. Substituindo x = 3 em qualquer das equações originais, encontramos y = 1. A solução é x = 3 e y = 1.

Sistema 3×3

Em sistemas 3×3, o processo se estende. Combinamos as equações aos pares, eliminando uma variável de cada vez até obter um sistema 2×2 e, posteriormente, um sistema 1×1. A organização estratégica das operações é fundamental para a eficiência do método. O objetivo é reduzir o sistema a uma forma triangular superior, facilitando a resolução.

Regra de Cramer

A regra de Cramer oferece um método elegante e direto para resolver sistemas lineares, utilizando determinantes. Para um sistema 3×3, calculamos o determinante da matriz dos coeficientes e os determinantes das matrizes obtidas substituindo cada coluna da matriz dos coeficientes pelo vetor dos termos independentes.Considere o sistema:

2x + y – z = 8
x – y + 2z = 3

x + y + z = 11

Calculamos o determinante da matriz dos coeficientes (D), e os determinantes das matrizes obtidas substituindo a coluna das x (Dx), y (Dy), e z (Dz) pelo vetor dos termos independentes. As soluções são dadas por x = Dx/D, y = Dy/D, e z = Dz/D. O cálculo dos determinantes envolve a aplicação da regra de Sarrus ou outras técnicas de cálculo de determinantes.

Método de Gauss-Jordan

O método de Gauss-Jordan, utilizando matrizes, representa uma abordagem sistemática e eficiente para resolver sistemas lineares. O processo envolve operações elementares sobre as linhas da matriz aumentada (matriz dos coeficientes concatenada com o vetor dos termos independentes) para transformá-la em uma matriz identidade na parte dos coeficientes. A solução aparecerá na coluna dos termos independentes.Considere o sistema:

x + y + z = 6
x – y + z = 2

x + y – z = 1

Construímos a matriz aumentada e aplicamos operações elementares como multiplicar uma linha por uma constante, somar um múltiplo de uma linha a outra, ou trocar duas linhas. O objetivo é obter uma matriz da forma [I | solução], onde I é a matriz identidade. Cada operação elementar corresponde a uma transformação equivalente no sistema linear original, mantendo a equivalência entre os sistemas.

A solução final será obtida diretamente da matriz transformada.

Tipos de Sistemas Lineares e suas Soluções: Sistemas Lineares: O Que São, Como Resolver, Tipos – Brasil Escola

A jornada pela compreensão dos sistemas lineares nos leva agora a um ponto crucial: a classificação desses sistemas de acordo com o número de soluções que apresentam. Entender essa classificação é fundamental para dominar a arte de resolvê-los e aplicar esse conhecimento em situações reais, desde a organização de um estoque até a previsão de demanda em uma empresa.

Prepare-se para desvendar os mistérios dos sistemas possíveis, impossíveis e indeterminados!

Sistemas Lineares Possíveis

Um sistema linear possível é aquele que apresenta pelo menos uma solução. Geometricamente, isso significa que as retas (no caso de um sistema 2×2) ou os planos (em sistemas com mais variáveis) se intersectam em pelo menos um ponto. Em um sistema 2×2 possível, as retas podem se cruzar em um único ponto, representando uma solução única. Imagine duas estradas que se cruzam em um único ponto: essa é a representação visual de um sistema possível com solução única.

Se pensarmos em um sistema 3×3, a solução única seria o ponto de intersecção de três planos no espaço tridimensional. A solução única, neste caso, seria um conjunto de valores que satisfazem simultaneamente todas as equações do sistema. Um exemplo de problema cotidiano seria determinar a quantidade de cada tipo de produto a ser produzido, considerando recursos limitados (matéria-prima, tempo de produção) para maximizar o lucro.

Neste caso, as equações representariam as restrições, e a solução seria a combinação ideal de produtos.

Sistemas Lineares Impossíveis

Ao contrário dos sistemas possíveis, os sistemas lineares impossíveis não possuem solução. Imagine duas retas paralelas em um plano: elas nunca se cruzam. Esta é a representação geométrica de um sistema impossível. Da mesma forma, em um sistema 3×3, os planos poderiam ser paralelos, ou dois planos poderiam se cruzar, mas o terceiro seria paralelo à reta de interseção dos outros dois.

Em qualquer caso, não haveria ponto de interseção comum a todos os planos. Um exemplo prático seria tentar encontrar valores que satisfaçam duas condições mutuamente exclusivas, como “x + y = 5” e “x + y = 7”. Não existe nenhum par de números que satisfaça ambas as equações simultaneamente. A tentativa de encontrar um ponto de equilíbrio entre demandas conflitantes em um projeto, por exemplo, poderia levar a um sistema impossível, onde não há solução viável que atenda a todas as restrições.

Sistemas Lineares Indeterminados

Os sistemas lineares indeterminados possuem infinitas soluções. Geometricamente, isso ocorre quando as retas (em um sistema 2×2) são coincidentes, ou seja, uma reta sobrepõe a outra. No caso de um sistema 3×3, poderíamos ter três planos coincidentes, ou dois planos coincidentes e um terceiro plano que os intersecta em uma reta. Em qualquer caso, há uma infinidade de pontos comuns a todos os planos ou retas.

Imagine um problema de misturas: se você precisa misturar dois tipos de café para obter um preço médio específico, existem infinitas combinações possíveis de quantidades de cada tipo de café que resultam no preço desejado. Outro exemplo seria a distribuição de tarefas em uma equipe, onde várias combinações de atribuições de tarefas resultam no mesmo tempo total de conclusão.

Características dos Tipos de Sistemas Lineares

Para resumir, vejamos as características principais de cada tipo de sistema:

• Sistema Possível (com solução única): As retas (ou planos) se intersectam em um único ponto. Número de soluções:
  1. Implicações geométricas: Interseção única.
• Sistema Possível (indeterminado): As retas (ou planos) são coincidentes. Número de soluções: Infinito. Implicações geométricas: Coincidência.
• Sistema Impossível: As retas (ou planos) são paralelas e não coincidentes. Número de soluções:
  0. Implicações geométricas: Paralelismo sem coincidência.