Exercícios De Regra De Três (Respostas Explicadas) – Toda Matéria – Exercícios De Regra De Três (Respostas Explicadas)
-Toda Matéria: embarque nesta jornada fascinante pelo universo da matemática! Descubra o poder da regra de três, uma ferramenta essencial que desvenda os segredos por trás de inúmeras situações do cotidiano, desde cálculos simples até problemas complexos. Prepare-se para dominar esta técnica e transformar desafios em oportunidades de aprendizado e crescimento, desvendando os mistérios dos números com clareza e precisão.
Vamos juntos desvendar os diferentes tipos de regra de três, aprendendo a aplicá-la em diversas situações práticas e cotidianas, com explicações detalhadas e exemplos que irão consolidar seu conhecimento.
Através de exemplos práticos, passo a passo, você irá entender a lógica por trás de cada tipo de regra de três (simples direta, simples inversa e composta). Dominará a arte de identificar as grandezas proporcionais, superando os desafios com confiança e desenvolvendo uma compreensão profunda dos conceitos matemáticos envolvidos. Este guia completo irá equipá-lo com as ferramentas necessárias para resolver problemas com eficiência e precisão, abrindo portas para um novo nível de compreensão matemática e proporcionando uma experiência de aprendizado enriquecedora e transformadora.
Tipos de Regra de Três e suas Aplicações
A regra de três, ferramenta fundamental da matemática, desperta, muitas vezes, um misto de fascínio e apreensão. Mas, compreendendo seus diferentes tipos e aplicações, descobrimos uma aliada poderosa na resolução de problemas do cotidiano e em diversas áreas do conhecimento. Esta jornada nos levará a dominar a arte da proporcionalidade, desvendando os segredos da regra de três simples e composta.
Regra de Três Simples Direta e Inversa
A regra de três simples se divide em dois tipos principais: direta e inversa. Na direta, o aumento de uma grandeza implica no aumento proporcional da outra, e vice-versa. Já na inversa, o aumento de uma grandeza acarreta na diminuição proporcional da outra. A compreensão dessa distinção é crucial para a correta aplicação da regra.
| Tipo | Fórmula | Exemplo | Solução Detalhada |
|---|---|---|---|
| Simples Direta |
a/b = x/y |
Se 5 máquinas produzem 100 peças em 2 horas, quantas peças 10 máquinas produzirão no mesmo tempo? |
5 máquinas — 100 peças Resolvendo a proporção: 5/10 = 100/x |
| Simples Inversa |
a*b = x*y |
5 pedreiros constroem uma casa em 10 dias. Quantos dias serão necessários para 2 pedreiros construírem a mesma casa? |
5 pedreiros — 10 dias Resolvendo a proporção inversa: 5*10 = 2*x |
Regra de Três Composta
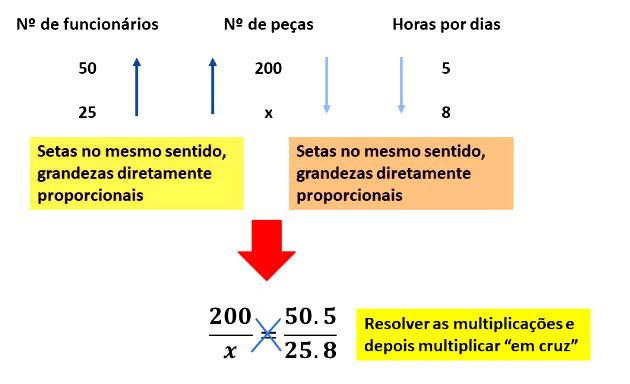
A regra de três composta lida com situações envolvendo mais de duas grandezas diretamente ou inversamente proporcionais. A chave para a resolução está em identificar a relação de proporcionalidade entre cada grandeza e a grandeza incógnita, organizando os dados de forma sistemática para encontrar a solução. Essa abordagem requer uma análise mais cuidadosa, mas a recompensa é a capacidade de resolver problemas complexos de forma eficiente.
| Tipo | Fórmula | Exemplo | Solução Detalhada |
|---|---|---|---|
| Composta |
Adaptação da regra de três simples, analisando as proporções de cada grandeza. |
10 operários constroem 2 casas em 15 dias, trabalhando 8 horas por dia. Em quantos dias 5 operários constroem 1 casa, trabalhando 6 horas por dia? |
Vamos analisar cada grandeza em relação ao número de dias (x): Montando a proporção: |
Diferenças entre Regra de Três Simples e Composta
A principal diferença reside no número de grandezas envolvidas. A regra de três simples relaciona apenas duas grandezas, enquanto a composta envolve três ou mais. Na simples, a proporcionalidade é direta ou inversa, enquanto na composta, pode haver uma combinação de ambas. A resolução da simples é mais direta, enquanto a composta exige uma análise mais detalhada das relações entre as grandezas para montar a proporção corretamente.
A regra de três simples é adequada para problemas com duas grandezas diretamente ou inversamente proporcionais, enquanto a composta é essencial para situações mais complexas com múltiplas grandezas.
Problemas de Regra de Três Simples com Soluções Passo a Passo

A prática é fundamental para consolidar o aprendizado. Os exemplos a seguir ilustram a aplicação da regra de três simples, passo a passo, permitindo que você internalize o processo e ganhe confiança na resolução de problemas.
Problema 1: Se 3 kg de maçãs custam R$ 12,00, quanto custarão 5 kg?
- Identifique as grandezas: kg de maçãs e custo.
- Verifique a proporcionalidade: direta (mais kg, mais custo).
- Monte a proporção: 3/5 = 12/x
- Resolva a proporção: 3x = 60; x = R$ 20,00
Problema 2: Uma torneira enche um tanque em 6 horas. Em quanto tempo 2 torneiras encherão o mesmo tanque?
- Identifique as grandezas: número de torneiras e tempo.
- Verifique a proporcionalidade: inversa (mais torneiras, menos tempo).
- Monte a proporção: 1*6 = 2*x
- Resolva a proporção: 6 = 2x; x = 3 horas
Problema 3: Um carro percorre 120 km com 10 litros de gasolina. Quantos litros serão necessários para percorrer 360 km?
- Identifique as grandezas: distância e litros de gasolina.
- Verifique a proporcionalidade: direta (mais distância, mais gasolina).
- Monte a proporção: 120/360 = 10/x
- Resolva a proporção: 120x = 3600; x = 30 litros
Problema 4: 8 costureiras produzem 40 vestidos em 5 dias. Quantas costureiras são necessárias para produzir 60 vestidos no mesmo tempo?
- Identifique as grandezas: número de costureiras e número de vestidos.
- Verifique a proporcionalidade: direta (mais costureiras, mais vestidos).
- Monte a proporção: 8/x = 40/60
- Resolva a proporção: 40x = 480; x = 12 costureiras
Problema 5: Um grupo de 6 pessoas consome 12 pizzas em 2 horas. Quantas pizzas um grupo de 3 pessoas consumirá no mesmo tempo?
- Identifique as grandezas: número de pessoas e número de pizzas.
- Verifique a proporcionalidade: direta (mais pessoas, mais pizzas).
- Monte a proporção: 6/3 = 12/x
- Resolva a proporção: 6x = 36; x = 6 pizzas
Resolvendo Problemas de Regra de Três: Exercícios De Regra De Três (Respostas Explicadas) – Toda Matéria
A regra de três, ferramenta poderosa para resolver problemas de proporcionalidade, desvenda os mistérios das relações entre grandezas. Domine-a e você abrirá portas para uma compreensão mais profunda do mundo quantitativo que nos cerca, desde o cálculo de ingredientes em uma receita até a previsão de crescimento populacional. Vamos desvendar seus segredos com um guia passo a passo, que transformará a resolução de problemas de regra de três em uma jornada fascinante e gratificante.
Resolvendo Problemas de Regra de Três Composta: Passo a Passo
A regra de três composta amplia o escopo da regra de três simples, permitindo lidar com problemas envolvendo mais de duas grandezas. A chave para o sucesso reside na identificação precisa das relações de proporcionalidade direta e inversa entre essas grandezas. Observe cada etapa com atenção, pois a prática leva à perfeição.
- Identificação das Grandezas: Liste todas as grandezas envolvidas no problema, identificando-as claramente. É fundamental compreender o que cada grandeza representa e como elas se relacionam.
- Proporcionalidade Direta ou Inversa: Analise cuidadosamente a relação entre cada grandeza e a grandeza que se deseja determinar. Se o aumento de uma grandeza implica no aumento da outra (mantendo as demais constantes), a relação é diretamente proporcional. Se o aumento de uma implica na diminuição da outra (mantendo as demais constantes), a relação é inversamente proporcional.
- Montagem da Proporção: Organize as grandezas em uma proporção, levando em conta a proporcionalidade direta ou inversa. Para grandezas inversamente proporcionais, inverta o valor de uma das razões.
- Resolução da Equação: Resolva a equação resultante da proporção, encontrando o valor da incógnita.
Ao identificar a proporcionalidade, lembre-se: grandezas diretamente proporcionais “andam juntas”, enquanto grandezas inversamente proporcionais “se opõem”.
Exemplo de Regra de Três com Grandezas Inversamente Proporcionais
Imagine que 5 trabalhadores constroem uma casa em 12 dias. Quanto tempo levarão 10 trabalhadores para construir a mesma casa, considerando que trabalham no mesmo ritmo?
| Etapa | Descrição |
|---|---|
| 1. Identificação das Grandezas | Grandezas: Número de trabalhadores (N) e Tempo (T) |
| 2. Proporcionalidade | Relação inversamente proporcional: Quanto maior o número de trabalhadores, menor o tempo. |
| 3. Montagem da Proporção | 5 trabalhadores / 10 trabalhadores = x dias / 12 dias (Inverte-se uma razão para refletir a proporção inversa) |
| 4. Resolução | 5
|
Note que invertemos uma das razões na proporção para refletir a relação inversamente proporcional. Essa inversão é crucial para a obtenção do resultado correto.
Problemas de Regra de Três com Soluções, Exercícios De Regra De Três (Respostas Explicadas) – Toda Matéria
Problema 1 (Simples Direta): Se 3 kg de maçãs custam R$ 15,00, quanto custarão 5 kg? Solução: 3 kg / 5 kg = R$ 15,00 / x => 3x = 75 => x = R$ 25,00 Problema 2 (Simples Inversa): Uma torneira enche um tanque em 6 horas. Quanto tempo levarão 2 torneiras iguais para encher o mesmo tanque? Solução: 1 torneira / 2 torneiras = x horas / 6 horas => 6 = 2x => x = 3 horas Problema 3 (Composta): 10 máquinas produzem 500 peças em 5 horas.
Quantas peças 15 máquinas produzirão em 8 horas? Solução: (10 máquinas / 15 máquinas)
- (5 horas / 8 horas) = 500 peças / x peças => (10/15)
- (5/8)
- 500 = x => x = 208,33 peças (aproximadamente).
Regra de Três e Situações do Cotidiano

A regra de três, ferramenta aparentemente simples, revela-se um poderoso aliado na resolução de problemas do nosso dia a dia. Sua capacidade de estabelecer proporções entre grandezas permite lidar com situações diversas, desde o preparo de receitas até o planejamento de viagens. Dominar essa técnica significa simplificar tarefas e tomar decisões mais assertivas no cotidiano.
Cinco Situações Cotidianas com Regra de Três
A aplicação da regra de três em situações cotidianas é vasta e surpreendente. Observemos cinco exemplos concretos de como essa ferramenta matemática se mostra útil e prática em nosso dia a dia.
- Situação 1: Preparo de Receitas: Uma receita de bolo exige 2 xícaras de farinha para 6 pessoas. Deseja-se fazer o bolo para 10 pessoas. Quantas xícaras de farinha serão necessárias?
- Definir as grandezas: xícaras de farinha e número de pessoas.
- Estabelecer a proporção: 2 xícaras / 6 pessoas = x xícaras / 10 pessoas.
- Resolver a equação: 6x = 20 => x = 20/6 = 10/3 ≈ 3,33 xícaras.
- Situação 2: Conversão de Moedas: Se 1 dólar equivale a R$ 5,20, quantos reais equivalem a 150 dólares?
- Grandezas: dólares e reais.
- Proporção: 1 dólar / R$ 5,20 = 150 dólares / x reais.
- Resolução: x = 150
– 5,20 = R$ 780,00.
- Situação 3: Consumo de Combustível: Um carro percorre 12 km com 1 litro de gasolina. Qual a quantidade de gasolina necessária para percorrer 180 km?
- Grandezas: quilômetros e litros.
- Proporção: 12 km / 1 litro = 180 km / x litros.
- Resolução: 12x = 180 => x = 180/12 = 15 litros.
- Situação 4: Escala de Mapas: Um mapa tem escala 1:100.000. Se a distância entre duas cidades no mapa é de 5 cm, qual a distância real entre elas?
- Grandezas: distância no mapa e distância real.
- Proporção: 1 cm / 100.000 cm = 5 cm / x cm.
- Resolução: x = 5
– 100.000 = 500.000 cm = 5 km.
- Situação 5: Compras no Supermercado: Se 3 kg de maçãs custam R$ 12,00, quanto custarão 5 kg?
- Grandezas: quilogramas e reais.
- Proporção: 3 kg / R$ 12,00 = 5 kg / x reais.
- Resolução: 3x = 60 => x = R$ 20,00.
Regra de Três e Porcentagens
A regra de três também se mostra uma ferramenta eficaz na resolução de problemas envolvendo porcentagens. A chave está em entender a porcentagem como uma razão entre duas grandezas.
| Situação | Resolução |
|---|---|
| Uma camisa custa R$ 80,00 e está com 20% de desconto. Qual o valor final? | Desconto: 20% de 80 = (20/100)
80 = R$ 16,00 80 – 16 = R$ 64,00 |
| Um investimento de R$ 1000,00 rendeu R$ 150,00 de juros. Qual a taxa de juros? | Taxa: (150/1000) – 100 = 15% |
Armadilhas e Erros Comuns na Regra de Três

Apesar de sua simplicidade aparente, a regra de três pode apresentar armadilhas para quem não a domina completamente. Um erro comum é a inversão das grandezas na proporção, levando a resultados incorretos. Outro equívoco frequente é a falta de atenção à unidade de medida, gerando confusão e cálculos imprecisos.
Para evitar esses problemas, é fundamental:
- Identificar claramente as grandezas envolvidas e suas unidades de medida.
- Verificar a proporcionalidade direta ou inversa entre as grandezas.
- Organizar cuidadosamente os dados em uma tabela para facilitar a visualização da proporção.
- Verificar a coerência do resultado obtido com o contexto do problema.

