Cálculo Diferencial e Integral de Várias Variáveis: Uma Introdução: Exemplo De Apicaçao Cálculo Diferencial E Integral De Várias Variáveis
Exemplo De Apicaçao Cálculo Diferencial E Integral De Várias Variáveis – O cálculo diferencial e integral de várias variáveis estende os conceitos do cálculo de uma variável para funções que dependem de duas ou mais variáveis independentes. Sua importância reside na capacidade de modelar e resolver problemas complexos em diversas áreas da ciência e engenharia, onde fenômenos são frequentemente influenciados por múltiplos fatores.
Introdução ao Cálculo Diferencial e Integral de Várias Variáveis
O cálculo de várias variáveis é fundamental para modelar sistemas físicos e processos em diversas áreas, incluindo física, engenharia, economia e ciência da computação. Compreender funções de várias variáveis, seus domínios, imagens, limites e continuidade é crucial para avançar em tópicos mais complexos.
Uma função de várias variáveis associa a cada ponto de um domínio um único valor na imagem. O domínio é o conjunto de todas as possíveis entradas da função, enquanto a imagem é o conjunto de todos os possíveis valores de saída. Limites e continuidade são conceitos importantes para analisar o comportamento de funções perto de pontos específicos do domínio.
Uma função é contínua em um ponto se o limite da função nesse ponto existe e é igual ao valor da função nesse ponto.
| Função | Domínio | Limite em (0,0) | Observações |
|---|---|---|---|
| f(x,y) = x² + y² | R² | 0 | Função contínua em todo R² |
| f(x,y) = xy/(x²+y²) | R² \ (0,0) | Não existe | O limite depende do caminho de aproximação |
| f(x,y) = e^(x+y) | R² | 1 | Função contínua em todo R² |
| f(x,y) = sen(x)cos(y) | R² | 0 | Função contínua em todo R² |
Derivadas Parciais e Diferenciais
As derivadas parciais representam a taxa de variação de uma função em relação a uma variável específica, mantendo as outras variáveis constantes. Geometricamente, a derivada parcial representa a inclinação da superfície representada pela função na direção de um eixo coordenado. As derivadas parciais são calculadas aplicando as regras de derivação de uma variável a cada variável, individualmente.
A diferencial total de uma função de várias variáveis aproxima a variação da função em resposta a pequenas mudanças em todas as suas variáveis independentes. Ela é uma generalização da diferencial de uma função de uma variável.
Em contraste com as derivadas de funções de uma variável, as derivadas parciais fornecem informações sobre a taxa de mudança da função em direções específicas (paralelas aos eixos coordenados). A diferencial total, por outro lado, fornece uma aproximação linear da variação da função para mudanças arbitrárias em todas as variáveis.
Aplicações da Derivada Parcial: Máximos e Mínimos
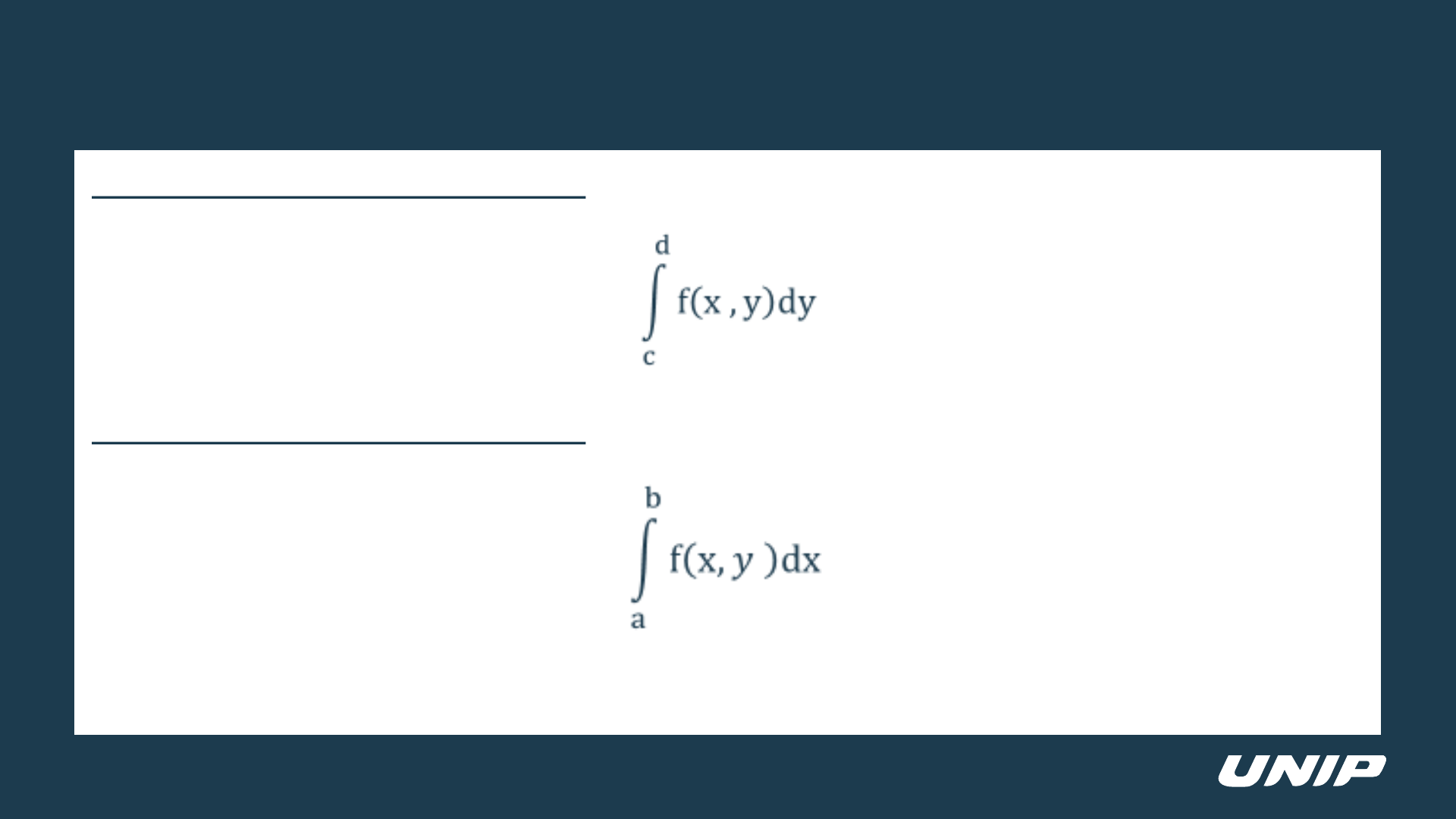
Encontrar máximos e mínimos de funções de várias variáveis envolve a identificação de pontos críticos, onde o gradiente da função é zero ou indefinido. O teste da segunda derivada, utilizando a matriz Hessiana, classifica esses pontos críticos como máximos locais, mínimos locais ou pontos de sela. Para problemas de otimização com restrições, o método dos multiplicadores de Lagrange é empregado.
- Encontrar pontos críticos: Calcular as derivadas parciais e resolver o sistema de equações resultante igualando-as a zero.
- Teste da segunda derivada: Calcular a matriz Hessiana e avaliar seu determinante e o traço nos pontos críticos para classificá-los.
- Multiplicadores de Lagrange: Introduzir multiplicadores para incorporar as restrições e resolver o sistema de equações resultante.
Exemplo: Encontre os pontos críticos de f(x,y) = x² + y²
-2x – 4y + 4 e classifique-os.
- Derivadas parciais: ∂f/∂x = 2x – 2; ∂f/∂y = 2y – 4
- Ponto crítico: (1,2)
- Matriz Hessiana: [[2, 0], [0, 2]]
- Determinante da Hessiana: 4 > 0 (mínimo local)
Integrais Múltiplas, Exemplo De Apicaçao Cálculo Diferencial E Integral De Várias Variáveis
Integrais múltiplas estendem o conceito de integração para funções de várias variáveis, permitindo o cálculo de volumes, áreas e outros tipos de quantidades em espaços multidimensionais. A integração iterada é o método principal para calcular integrais duplas e triplas. A escolha do sistema de coordenadas (retangular, polar ou cilíndrico) depende da geometria da região de integração e da função integrando, otimizando o processo de cálculo.
| Sistema de Coordenadas | Elemento de Área/Volume | Exemplo de Integral Dupla | Exemplo de Integral Tripla |
|---|---|---|---|
| Retangular | dx dy (ou dx dz dy, etc.) | ∫∫R x²y dx dy | ∫∫∫V x²y²z dx dy dz |
| Polar | r dr dθ | ∫∫R r²cos²θ r dr dθ | – |
| Cilindrica | r dr dθ dz | – | ∫∫∫V r²cos²θ z r dr dθ dz |
Para uma região de integração tripla em coordenadas cartesianas, a representação gráfica envolve a definição dos limites de integração para x, y e z. A forma geométrica da região pode ser um paralelepípedo, uma esfera, um cone, ou uma forma mais complexa, definida pelas inequações que delimitam a região. Os limites de integração refletem essas inequações, determinando a ordem de integração e os intervalos para cada variável.
Teorema de Green, Teorema de Stokes e Teorema da Divergência
Esses teoremas estabelecem relações importantes entre integrais de linha e integrais de superfície, simplificando cálculos em situações específicas. O Teorema de Green relaciona uma integral de linha ao redor de uma curva fechada plana com uma integral dupla sobre a região delimitada pela curva. O Teorema de Stokes relaciona uma integral de linha ao redor de uma curva fechada espacial com uma integral de superfície sobre uma superfície delimitada pela curva.
O Teorema da Divergência relaciona uma integral de superfície fechada com uma integral tripla sobre o volume delimitado pela superfície.
As semelhanças entre os três teoremas residem em sua natureza fundamental como teoremas integrais que relacionam integrais em dimensões diferentes. As diferenças estão na dimensão dos espaços envolvidos (2D para Green, 3D para Stokes e Divergência) e nos objetos matemáticos relacionados (curvas, superfícies, campos vetoriais).
Aplicações em Problemas de Engenharia e Física
O cálculo de várias variáveis tem aplicações cruciais em diversas áreas da engenharia e física. Na mecânica dos fluidos, é usado para modelar o fluxo de fluidos, utilizando equações como a equação de Navier-Stokes. Em eletromagnetismo, auxilia na análise de campos elétricos e magnéticos, com a lei de Gauss e a lei de Ampère. Em transferência de calor, o cálculo é fundamental para modelar a condução, convecção e radiação de calor.
Exemplo em Mecânica dos Fluidos: A equação de continuidade, ∇ ⋅ v = 0, onde v é o campo de velocidade do fluido, descreve a conservação de massa em um fluxo incompressível. Esta equação utiliza o operador divergência, um conceito fundamental do cálculo vetorial.
Quais são as principais dificuldades enfrentadas ao aprender cálculo de várias variáveis?
Visualização espacial e abstração matemática são os principais desafios. A generalização de conceitos unidimensionais para múltiplas dimensões exige um esforço extra de compreensão.
Como posso praticar e melhorar meu entendimento do cálculo de várias variáveis?
Resolva muitos exercícios, utilize softwares de visualização gráfica e procure por explicações alternativas em diferentes fontes. A prática consistente é fundamental.
Quais são as aplicações mais relevantes do cálculo de várias variáveis na indústria?
Otimização de processos, modelagem de sistemas dinâmicos, análise de dados e simulação computacional são algumas das aplicações mais relevantes em diversos setores industriais.

