Divisão: Uma Exploração Completa: Como Fazer Uma Divisão Por Exemplo 3 Dividido Por 4
Como Fazer Uma Divisão Por Exemplo 3 Dividido Por 4 – A divisão é uma operação aritmética fundamental que representa a distribuição equitativa de um valor em partes iguais. Ela está intrinsecamente ligada à multiplicação, subtração e ao conceito de fração, servindo como ferramenta essencial em diversas situações do dia a dia, desde o compartilhamento de alimentos até cálculos complexos em engenharia.
Introdução à Divisão
A divisão pode ser entendida como a operação inversa da multiplicação. Se 4 multiplicado por 3 é igual a 12 (4 x 3 = 12), então 12 dividido por 4 é igual a 3 (12 ÷ 4 = 3). Ela também pode ser vista como uma subtração repetida até que o valor seja menor que o divisor. Frações representam a divisão de um número por outro, onde o numerador é o dividendo e o denominador é o divisor.
No cotidiano, dividimos fatias de pizza entre amigos, calculamos a média de notas ou dividimos custos em grupos.
| Dividendo | Divisor | Quociente | Resto |
|---|---|---|---|
| 10 | 2 | 5 | 0 |
| 11 | 3 | 3 | 2 |
| 25 | 4 | 6 | 1 |
| 30 | 5 | 6 | 0 |
Método Tradicional de Divisão (3 ÷ 4)
Para dividir 3 por 4 usando o método tradicional, observamos que 4 não cabe nenhuma vez inteira em 3. Portanto, o quociente é 0 e o resto é 3. Isso pode ser representado pela fração 3/4. A divisão de números inteiros resulta em um quociente inteiro e um resto, enquanto a divisão de números decimais pode resultar em um número decimal como quociente.
Em 3 ÷ 4, o quociente é 0 e o resto é 3. A representação fracionária é 3/4. Ao comparar com a divisão de números decimais, obtemos 0,75 (como veremos na próxima seção).
Representação Decimal da Divisão, Como Fazer Uma Divisão Por Exemplo 3 Dividido Por 4
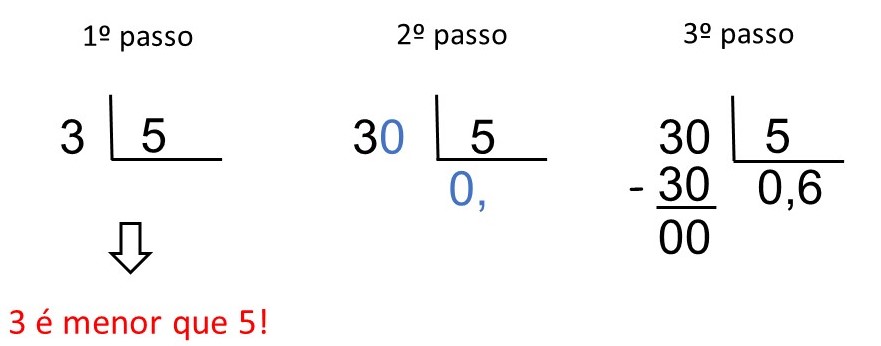
A fração 3/4 pode ser convertida em um número decimal através da divisão do numerador (3) pelo denominador (4). Dividindo 3 por 4, obtemos 0,75. Números decimais são representados por uma vírgula separando a parte inteira da parte fracionária.
- Divida o numerador (3) pelo denominador (4).
- Adicione um zero ao dividendo (3) e continue a divisão.
- O resultado será um número decimal (0,75).
Divisão como Fração e Porcentagem

A divisão 3 ÷ 4 é representada pela fração irredutível 3/
4. Para converter essa fração em porcentagem, multiplicamos a fração por 100%: (3/4) x 100% = 75%. A representação da divisão como fração (3/4), decimal (0,75) e porcentagem (75%) são equivalentes, apenas com diferentes formas de representação.
Aplicações Práticas da Divisão (3 ÷ 4)
A divisão 3 ÷ 4 encontra aplicações práticas em diversas situações. Veja três exemplos:
| Cenário | Cálculo | Resultado | Interpretação |
|---|---|---|---|
| Dividir 3 pizzas entre 4 pessoas | 3 ÷ 4 = 0,75 | 0,75 pizzas por pessoa | Cada pessoa recebe 3/4 de uma pizza. |
| Desconto de 75% em uma compra de R$3,00 | 3 x (75/100) = 2,25 | R$2,25 de desconto | O valor do desconto corresponde a 3/4 do valor total. |
| Distribuir 3 litros de tinta em 4 paredes | 3 ÷ 4 = 0,75 | 0,75 litros por parede | Cada parede recebe 3/4 de litro de tinta. |
Problemas com Divisão e Restos

Problemas envolvendo divisão com resto são comuns em diversas áreas. A interpretação do resto é crucial para a solução correta.
- Problema 1: Uma caixa comporta 4 bombons. Quantos bombons cabem em 7 caixas e quantos bombons sobram? Solução: 7 x 4 = 28 bombons; não há sobras.
- Problema 2: Ana tem 11 balas e quer dividi-las igualmente entre 3 amigos. Quantas balas cada amigo recebe e quantas sobram? Solução: 11 ÷ 3 = 3 balas por amigo com 2 balas restantes.
- Problema 3: Um grupo de 15 pessoas precisa ser dividido em equipes de
4. Quantas equipes completas podem ser formadas e quantas pessoas sobrarão? Solução: 15 ÷ 4 = 3 equipes com 3 pessoas restantes.
Dividir 3 por 4, aparentemente simples, nos conduziu por um caminho rico em conceitos matemáticos. Do método tradicional à representação em frações, decimais e porcentagens, exploramos a flexibilidade e a aplicabilidade dessa operação em diferentes contextos. Compreender a divisão não se limita à obtenção de um resultado numérico; trata-se de internalizar a lógica subjacente e a capacidade de interpretar o quociente e o resto, ferramentas essenciais para a resolução de problemas em diversas áreas.
Esperamos que esta análise tenha clareado o processo, fortalecendo sua compreensão e preparando-o para enfrentar novos desafios matemáticos com confiança e precisão. A matemática, afinal, está em todos os lugares – e agora você está mais bem equipado para decifrá-la.

